Dear lord.
Apparently another “viral math problem” is on the loose. Let’s see…

Oh no…
The reason I dread it is because there was one from the year before that is basically identical aside from the numbers:
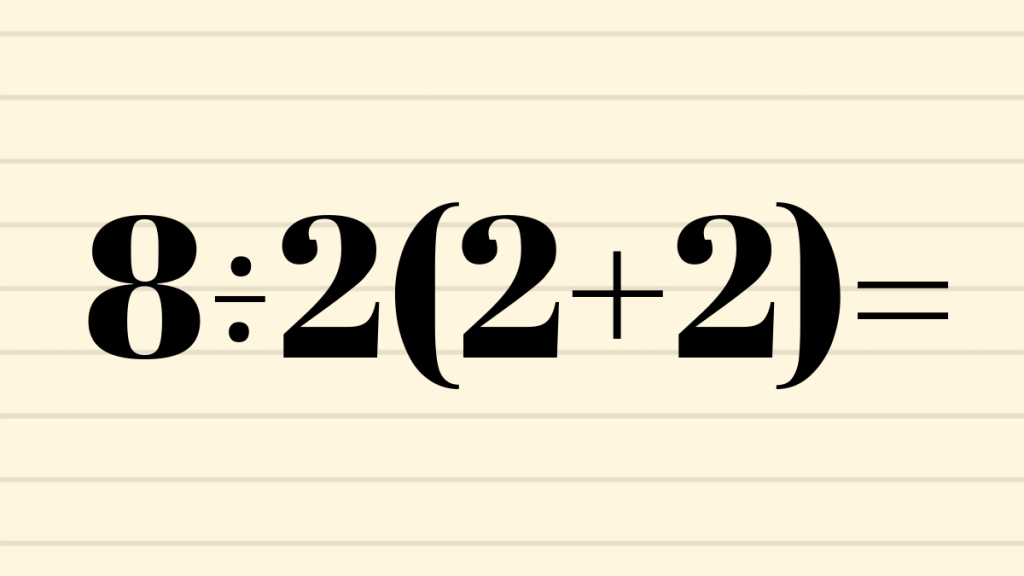
Ugh… why do I hate these types of “problems”? They’re purposefully ambiguous to effectively divide the internet, pun intended. Wait… there’s a pun in saying that? Yes. The division symbol is the cause. Like, THE cause.
Let’s get into the math behind it. To start, everyone generally will immediately yell, “It’s easy, guys. Just use PEMDAS! It’s so easy, bro…” Well… sure, although GEMDAS is a better way of dictating order, and even then, there’s still deception in how the order is posed. But how does PEMDAS/GEMDAS work?
-G for Grouping Symbols (Like parentheses, brackets)
-E for Exponents
-M for Multiplication
-D for Division
-A for Addition
-S for Subtraction
Grouping Symbols are first, then Exponents. But here’s the tricky part: Multiplication and Division are interchangeable, as are Addition and Subtraction, meaning the operations from that point go left to right. For example, if given 6 / 2 x 3, the division goes first, then multiplication, meaning the expression evaluates to 9.
The reason why these operations are considered interchangeable is that they are inverse operations. I even remember talking about this with high school seniors once. So, for example, why does, for example 4 – 5 + 3, evaluate to 2 and not -4? Well, the -5 is actually a + (-5). Thus, 4 – 5 + 3 is equal to a 4 + (-5) + 3, thus, no matter which addition operation is performed first (as addition is associative), the expression will evaluate to 2. So on the earlier example with the multiplication and division, what’s really happening is that /2 is really x0.5, thus making it 6 x 0.5 x 3, which always evaluates to 9 (as just like addition, multiplication is associative because multiplication is “repeated addition”).
The choice for that multiplication/division example is because they match the numbers from the “viral” problem. Based on the presentation, any operation in the grouping symbols get performed first, so 1+2=3. Alright, seems simple enough. But here’s where it’s hairy: do we go multiplication first or division first? Well, based on what we’ve done so far, it seems like we have 6 / 2 x 3, which we’ve concluded is 9. Alright, there’s answer! It’s 9…
…well, not so fast. There’s a strong contention from some people that the answer is really 1. This largely comes from doing multiplication first, then the division: 2×3=6, then 6/6=1. Now I know what you might be thinking: we just concluded that it’s 9 from before! Multiplication and Division goes left to right! Well, yes, but if we look at the original expression, we have a 2 right next to the left parenthesis. Generally, we imply this to mean multiplication. Oh, so distribute? Well that will lead to a 1. But wait… do we really want to do that first? It almost seems like it is because of how the 2 is paired with the left parenthesis. But if that REALLY was to be the case, another pair of grouping symbols SHOULD have been placed around that entire “block” (which would then exclude the division symbol and 6).
One other major complaint for this is the use of the division symbol: if anyone can recall anything about that symbol, it’s that we usually stop seeing it by the time we start 6th grade, and if not by then, by whenever we start Pre-Algebra (which usually falls in 7th grade). Because by that point, what do we start using? Fraction bars. Yea, those dreaded fractions. With a fraction bar, the problem gets eased because it becomes CRYSTAL CLEAR what has to happen first. For example, with this:
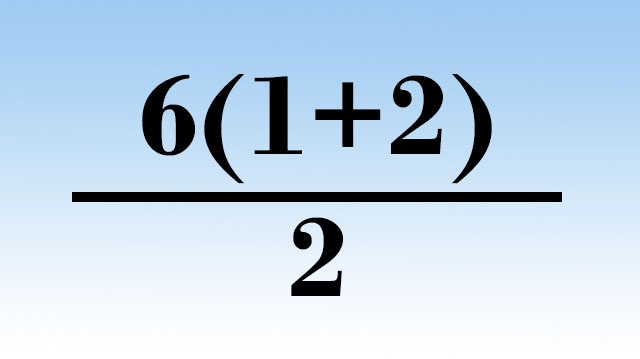
We know that the expression in the numerator gets evaluated first, so here, it can only evaluate to 9. If the (1+2) were to be in the denominator, however, we’d instead evaluate to 1.
One brief note on the URL in the caption: it’s from 2017. This problem has popped up before. And I can’t leave the URL in full here because it has NSFW language, which I will keep off this website. Nonetheless, worth a read (although it tries to enforce the 9 answer which I think betrays the moral of the problem, which is to not care about these types of problems).
OK. So knowledge of mathematics by hand seems to be ambiguous. What about a calculator? That should end the debate, right? Well… even there it’s ambiguous. Wait… what? A TI-84 CE will spit out a 9. A Casio fx-115MS will spit out a 1. So even calculators can’t seem to agree.
So what have we learned? Problems like these are needless. They only serve to trip people up, stir up arguments, and lead to a whole lot of nonsense.