If you’re here from LaserBelch’s stream, I bet you read that title with his notification alert.
Anyway, there’s something to be said about my fascination with prime numbers. Recall that a prime number is a natural number with exactly two factors: 1 and itself.
It all starts back in second grade when I had a math enrichment tutor. One lesson, my tutor taught me about what prime numbers were and gave me the list of prime numbers less than 100: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
As numbers have generally been pretty easy for me to remember, I’ve known this list by heart since it was first given to me. It didn’t help that in the next few years, I continued to practice my knowledge with a very old math educational game known as Number Munchers.
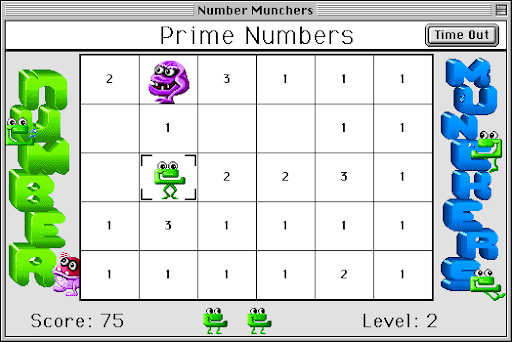
I might not have been playing on the oldest port as an elementary school student (Mac OS 9), it bears mention that it is a VERY old game dating to 1987. Every so often we’d be going to the computer lab to play Number Munchers to practice our math skills. Given that I had thorough knowledge of what primes were (relative to my peers), I could jump into the Prime Numbers game mode easily and munch away. In fact, whenever I watched my classmates play, I was known as the one who’d say that they munched on the wrong numbers. In fact, one of them even wrote about it in a skit about the class, where “I was yelling that 9 was not a prime”.
I guess I can talk about Number Munchers itself. It’s a survival game where you control the eponymous Muncher on a 6×5 grid as it munches away at the numbers that satisfies the condition based on the game mode. For example, in Multiples mode, the Muncher has to eat multiples of a given number, while in Equality mode, the Muncher has to eat expressions equal to a given number. In Primes mode, which was my specialty (and remains so to this day), the Muncher merely has to eat the prime numbers on screen.
But why is this game “survival”? Well, the Muncher has a limited amount of lives and has to avoid eating wrong numbers (at the cost of a life) as well as the enemies of the game: Troggles. There are five types of troggles in the game that will eat the Muncher as soon as they occupy the same space, and they all have mock-binomial names: Reggies (Trogglus normalus), Helpers (Trogglus assistus), Workers (Trogglus laborus), Bashfuls (Trogglus timidus), and Smarties (Trogglus smarticus). The game ends as soon as all lives are lost, and lives aren’t particularly easy to come by (only by attaining a certain scoring threshold).

Depending on which port you have, it is also possible to set the content in the game modes, such as having the levels get progressively harder by slowly introducing larger numbers. A great way to develop memory of the primes is to have that set, as in Level 1, there are only 1s, 2s, and 3s, but by Level 36 or so, numbers around 150 are on the field as well. The limit is generally around 200 or so (meaning the highest prime to munch on is 199).
Anyhow, I’d like to talk about an algorithm to determining primes which segues into the next game I’d like to discuss: the Sieve of Eratosthenes. The steps are as follows:
1) Set a maximum number “n”.
2) List all natural numbers from 1 to n.
3) Box the prime numbers less than the square root of n.
4) Start crossing off multiples of the boxed numbers.
5) Any number (aside from 1) that is not boxed or crossed off is a prime.
So, for example, with 101, the boxed numbers are 2, 3, 5, and 7 (as the square root of 101 is just a hair greater than 10). From that point, once the crossing off of numbers finishes, we’re left with the same list of numbers for that of 100, although this time, 101 was not crossed off, leaving it to be prime as well.
What’s interesting is that the Sieve used on 101 is cleverly hidden in a board game known as Prime Climb:

Notice how the board makes note of which numbers are marked as multiples of 2, 3, 5, and 7. For example, with 84: It has two orange marks, one green mark, and one purple mark. Consider this: 2 x 2 x 3 x 7 = 84. So, not only does the board act as a Sieve of Eratosthenes acting on 101, it also includes the prime factorization of every composite number less than 101 (Recall that a composite number is a number that isn’t prime that has 3 or more factors).
I guess I can speak about the game, because in all honesty if played with a group of friends, trolling awaits based on the rules. Each player starts with two pawns of a color and the goal is to advance both pawns to 101. Each turn consists of four phases: Roll, Move, Bump, and Draw, the last two occuring if applicable.
The movement all lies on the roll of the two ten-sided dice provided (precisely, two pentagonal trapezohedrons for those who know how to name polyhedra or two d10s for those who play Dungeons & Dragons). You get to move a pawn by adding, subtracting, multiplying, or dividing the number it is on using the numbers from the rolls (the 0 on a die is meant to represent 10). The interesting thing is that a pawn may move twice or one number is used for one pawn with the other number saved for the other.
Now Bumping is a phase that can only occur if two pawns occupy the same space. The pawn that moves in stays, while the pawn that was there gets “bumped” back to start (at 0), and this, to me, is where the trolling happens (although it is possible to bump your own pawns), as bumping is mandatory whenever it occurs.
The last phase, Drawing, involves drawing a Prime Card. There are two types of Prime Cards: Actions, which you play immediately, or Keepers, which you play during your next Move phase (you must also keep it face up in your possession). Although there are no restrictions on how many Keeper Cards you can activate or keep, there are restrictions to drawing Prime Cards in general:
-If a pawn lands on a red space (and it can ONLY be red), you draw exactly one card.
-If a pawn returns to the red space that it started on that turn, you do not draw a card.
-If both of your pawns land on red spaces, you only draw one card.
-If an action card moves one of your pawns to a red space, you do not draw a card.
-If you land on 101, you do not draw a card.
Once a pawn lands on 101, it moves off the board. The goal, as mentioned before, is to have both pawns land on 101 to win the game before the other players.
Down the road I hope to be able to enjoy this game with people more. Additionally, I hope folks become acquainted with Number Munchers so that we can revive interest in it, because it’s pretty good practice for wee tots in elementary school. If you want a place to play it, though, the Internet Archive has it.
Enjoy that Prime… GAMING!