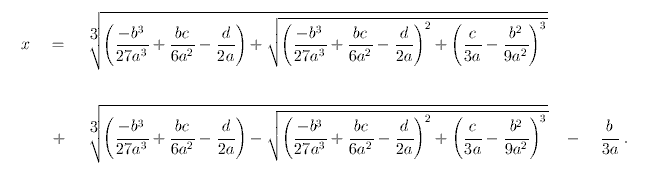I recently came across a video discussing the Cubic Formula, specifically the one published by Italian mathematician Gerolamo Cardano.
Before I talk about the video, I would like to talk a bit about the channel. The eponymous mathologer, Burkard Polster, is a mathematics professor at Monach University in Melbourne, Australia. He has uploaded a multitude of videos discussing other mathematics topics, including one where he provided a lengthy critique of another video by Numberphile, another YouTube channel known for mathematics videos. One of the top rated comments on this video called it “the math equivalent of a diss track”.
As for the video, Polster discusses in great length how Cardano derived the formula. Due to the nature of the mathematics and how dense it is, I recommend any potential viewer to set aside about an hour and a half to watching it, as it may be necessary to pause at various points. Additionally, there’s a dedicated chapter to addressing the question of why it’s not taught in schools, an aspect which I took great intrigue in.
Relying on my own experience, I remember skirting over it in my Elementary Functions class in junior year of high school (and possibly my Algebra II class the previous year) as my teacher mentioned that a cubic formula existed but it was incredibly long and needless to teach, although he had it written on paper for us to see at the end of class. Based on how I remembered looking at that paper then, I can recall I was like, “…yea nope.”
When it came to the idea of deriving it, I personally think it’s natural to wonder why it isn’t taught considering how the quadratic formula is a staple of Algebra II classes nowadays. Yes, it’s a necessary topic that every aspiring STEM career student needs it in their toolbox, yet there’s a tool to allows nearly everyone to remember it… a song set to the melody of “Pop Goes the Weasel”:
So when we actually look at how dastardly Cardano’s cubic formula looks…
It’s easy to see why a composing a song might prove to be a daunting task. Not only that, the formula itself is composed of an astounding amount of coefficients, not to mention a square root within each cubic root. Additionally, as discussed in the video, there’s a potential to encounter complex numbers because of the presence of a square root, something that is not really taught beyond a surface level while learning quadratic functions. One other important factor towards not teaching this is that by the end of Pre-Calculus, more efficient methods are taught (Polynomial Division and Synthetic Division) that potentially allow for the calculation of all the roots as opposed to just one.
This poses an interesting question of why Cardano’s cubic formula only gives one solution. Well, for one, the video explains how that is so, but in short, due to the nature of cubic functions, one root is always guaranteed. In fact, based on how the derivation process, the formula is guaranteed to evaluate to a real solution.
I can also say that I also went through the process of writing my own derivation of the formula based on the video. In my own drawing notebook, I spent 4.5 pages writing down a proof (counting front and back as two pages), while in LaTeX (a software that a lot of academia use to produce STEM documents), it took about 6.5 due to formatting. As noted in the video, some Calculus is actually required to derive the formula (specifically knowledge of derivatives and the calculation of inflection points). However, where the derivation became very intensive once I had to deal with roots, and I needed to define coefficients for root terms to ease up potential confusion. Overall, this process took several hours in total over the course of a few nights.
So overall, this experience has been extremely enlightening and I hope to find more topics to talk about on the blog. Perhaps more videos or other fun topics?